Feedback and Stability

The Moon’s uneven gravity field causes most lunar orbits to be unstable. Over time the orbits increase in eccentricity, which is to say that the high part of the orbit gets higher, and the low part gets lower, until the object strikes the lunar surface. In this blog I have described the orbits of two different Apollo artifacts that show long-term stability in their orbits. (The Eagle and Snoopy.) They somehow manage to evade the instability that dooms most lunar satellites. How could that be? In this post we’ll dig in deeper to try to understand what is going on in greater detail.

I’ll start by focusing on the Eagle, and then at the end we can do a similar analysis for Snoopy. To start, as a reminder, look at the way the perilune altitude varies over time in the figure below. (Remember, perilune altitude is the lowest point of each revolution.) You see a cycle that repeats as the minimum altitude dips lower then climbs higher about every 25 days. I showed in a previous post that this 25-day cycle reflects the way the orbit changes as the Moon rotates underneath. The lowest lows always occur on the near side of the Moon. The fact that the cycle completes in 25 days, while the Moon completes a full rotation in 27.32 days, means that the Eagles orbit is also precessing. (This is also sometimes called “Apsidal advance”.) In this way the long axis of the Eagle’s orbit, called the Apse Line, does a complete circuit of the Moon in about 25 days, and this drives the short-period variation.

Figure 1: Minimum altitude of the Eagle in the first year after jettison. Notice the shorter variations every 25 days, and the longer variation every 4-5 months.

What about that longer variation in the perilune altitude? Notice how every 4-5 months the minimum altitude goes higher and then lower. What’s going on there? If you look at the figure above, notice that the minimum altitude is nearly the same at point A and point B, but somehow this system “knows” that at point A the longer cycle is increasing, and at point B the longer cycle is decreasing. Somehow there is “state” information being stored in the system, so that it “remembers” where it is in the long-period cycle. Let’s dig in and look for that “state” signal.

Figure 2: Showing the time (in days) between the peaks of the first 4 complete cycles for the Eagle. Notice that the time between peaks increases as the altitudes move lower.

For starters, let's look for differences between the “low” cycles and “high” cycles. One thing to measure is the “period” of the cycle, i.e., how many days it takes to complete a cycle. We can measure the time between the highest point in each cycle. In figure 2 above, I show the time (in days) to go from one peak to the next for the first 4 complete cycles of the Eagle’s orbit back in 1969. Do you notice anything interesting? As the altitudes get higher, the times get a bit shorter. As the altitudes get lower, the times get a bit longer. We can plot these on a graph that makes the relationship easier to see, and in the figure below I show the first 14 cycles…the first year of the Eagle after jettison. If I plotted out the data for 52 years you would see that the same relationship continues to the present day. This is a persistent feature of the Eagle's orbit.

Figure 3: Cycle length and end peak altitude for 14 Eagle cycles during its first year in lunar orbit.

The next thing to notice about these cycles is how they relate to the Moon. The plot below shows perilune altitude versus the Moon’s longitude, for one year. As the Moon rotates underneath the orbit, we see 14 tracks wrapping around. Each of the blue dots represents the lowest point of one revolution, and the longitude where that low point occurs above the Moon. What’s interesting is that the lowest parts of the cycles always occur on the near side of the Moon, near 30 degrees East, while the highest parts occur on the lunar far side. (From Earth we can only see lunar longitudes between -98° and +98°.)

Figure 4: Mapping how perilune altitude varies with lunar longitude. Eccentricity of the orbit is highest when perilune occurs on the near side of the Moon.

You might also notice some “sloshing” back and forth in that pattern in Figure 4. Notice on the left part of the figure where the highest points in each cycle are marked with red dots. The dots actually form a loop. It's even more interesting to connect the successive dots, as in Figure 5 below. In this figure I’m only showing the highest points of each cycle, like the red dots above, but now I added a dotted blue line showing the sequence. You can see that over the course of a year these dots trace out a series of loops. And these loops tie back to the slower 4- to 5-month variation you see that first figure above. Now we can see the difference between points A and B in the first figure. I’ve marked them again in Figure 5. Point A occurs about 30 degrees farther to the East than point B. This longitudinal variation is how the system stores its “state” information…how it “remembers” whether the short cycles are increasing or decreasing. And just to be clear, this is another pattern that is stable over decades. On the left in Figure 5, notice how this variation looks over a 50-year period. It doesn’t expand or contract or drift away. It remains centered on this longitude.

Figure 5: These plots show the lunar longitude where the perilune cycle peaks occur. Points A and B on the left are the same ones marked in Figure 1. All the red points on the left are also marked in red in Figure 4. Data for 50 years is plotted on the right, showing the long-term stability of the pattern.

We’ve seen how the eccentricity variation of the orbit stays locked to lunar longitude over decades. How can that be? There must be some feedback mechanism that prevents it from drifting away. It’s interesting to look at the rate that the perilune longitude point changes. To do that, for every revolution, we have to measure how far Eastward the perilune point shifted and compare that to the elapsed time. If we divide the longitude change by the elapsed time, we get a measure of the rate. (The elapsed time is nearly constant…about 1 hour and 58 minutes per revolution, but it’s a spreadsheet doing the math, so why not recalculate it for each point.) I’ll call this measurement the “precession rate”. That’s kind of a misnomer…the longitude is mostly changing because of the Moon’s rotation under the orbit, which is not really precession. (This component is also constant, because the rate of the Moons rotation is constant.) But there is an additional precession in the orbit so there is some variation in this precession rate. Here it is...

Figure 6: The "Precession Rate" varies depending on perilune altitude.

What is interesting here is that the rate gets much faster as the perilune altitude gets higher. Put another way, the precession rate varies inversely with eccentricity. As the orbit becomes more eccentric, the rate slows down. As the rate slows down, the Moon's gravity begins to drive the eccentricity lower. Lower eccentricity causes the rate to speed up, and the cycle repeats. Again, and again. For decades.

OK we found an interesting pattern in the orbit of the Eagle that persists for decades and can plausibly explain its long-term stability. (“Explain” is a strong word here…I believe there are more layers to this onion.) How about the Snoopy descent stage? If we go through the same exercise with Snoopy, we see very similar patterns. Compare the figures below for Snoopy’s orbit to those above for the Eagle. There is something about these retrograde equatorial orbits that leads to long-term stability, somehow evading the unstable fate of most other lunar satellites. Pretty cool, eh?

Figure 7: These plots of Snoopy's orbit data show similar patterns to those of the Eagle. A similar feedback mechanism seems to be responsible for the long-term stability displayed by both orbits.

Has the Eagle Landed?

 No one knows what became of the Eagle. That seems wrong. 

After it carried Neil Armstrong and Buzz Aldrin back from the surface of the Moon in 1969, the ascent stage of the Apollo 11 Lunar Module "Eagle" was jettisoned into lunar orbit. The astronauts watched out the window as it drifted away. The NASA tracking network followed it for a few revolutions, until they lost the signal. Since then no one has seen or heard from the Eagle. Without question it is one of the most important machines ever created by humanity. Not knowing her fate is a terrible wrong which must be righted.

The assumption has always been that the Moon's lumpy gravity caused the Eagle's orbit to decay, and she impacted the Moon at an unknown location. In this post I will go through the last known orbital state of the Eagle, and show the results of simulating that orbit with the best gravity models available. Spoiler alert: as I found previously with "Snoopy", the orbit is quasi-stable. Lunar gravity alone may not have brought the Eagle down.

For the orbital state of the Eagle at the time it was jettisoned, we look to the Apollo 11 Mission Report. Table 7-II lists information about the spacecraft at various points in the mission, and in particular there is an entry for "Ascent stage jettison" as below.

Orbital State of the Eagle at jettison, from the Mission Report

As I have described in a previous post, I use a simulation tool developed by NASA, and gravity models derived from GRAIL data. It's fairly straightforward to plug in the values from the table and simulate the stage. There is one problem with the Mission Report, though. It's wrong! When you think back to 1969, a world where word processing does not yet exist, and data processing is cumbersome, it isn't shocking that there is a problem in the table. But if you know a bit about the Apollo 11 orbit, the error is rather glaring.

All of the Apollo missions followed orbits that were low in inclination...that is, they stayed close to the lunar equator. It means that their "Space-fixed heading angle East of South" in degrees was never far from -90 degrees. If we use the value in the table, the orbit is inclined to the lunar equator by about 8 degrees...it can't be right.

What to do? Fortunately there is another source. This paper from 1970 lists orbit data for several Apollo missions, including Apollo 11. In particular, it lists the inclination for several revolutions leading up to the moment the Eagle was cast off. By plotting out the values and extrapolating, one can find an accurate inclination at that moment...178.817 degrees. (Inclination would be 0 degrees for an orbit following the lunar equator, in the direction the Moon rotates. Because the orbit is "against" the rotation, the inclination is close to 180 degrees.) Using GMAT this inclination can be translated into a heading angle...-89.63 degrees.

Extrapolating to find the inclination at the moment of jettison

Plugging this value into GMAT, along with the other values from table 7-II leads to a simulated orbit that matches up nicely to what is known about the mission. For instance the ground track of the orbit matches up well with those depicted in the Mission Report; the apolune and perilune values agree with values reported by Public Affairs Officer during the mission; and longitude values from the simulation agree well with Aquisition Of Signal and Loss Of Signal (AOS/LOS) times reported by tracking.

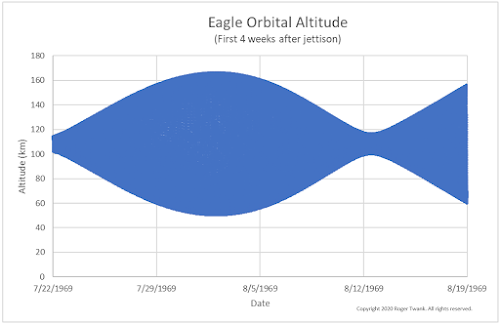
So what happens to our simulated Eagle? Let's look at the first five days after jettison. The stage was initially in an orbit that was "63.3 by 56 nautical miles", according to a P.A.O. announcement a few hours after jettison. That's a nearly circular orbit that is 117.2 kilometers at the high point and 103.7 km at the low point. From there we can see that our simulated stage is pulled into a more eccentric orbit, with higher highs and lower lows over the next 5 days.

If this trend were to continue, the Eagle would have indeed impacted the moon within a few weeks. However, as I have seen in previous simulations of Snoopy, there is a pattern that takes hold, and the orbit cycles through periods of higher and lower eccentricity, completing one cycle about every 22 days. In the plot below we see that after about 10 days, the orbit begins to return to a more circular pattern, with lower highs and higher lows, until around August 13th, when it is nearly back to the original state. Then a new cycle begins and we see the minimum altitude dropping again.

For simplicity in the plots below, I will ignore the higher parts just focus on the lowest points of each orbit, following the lower envelope of the plot. If I plot out these low points (the "perilune" points) for the first year, we see that the orbit continues to oscillate throughout the year.

What is exciting about this simulation is that there is no impact! Across the first three cycles of eccentricity, the low point of the orbit drops down to within 20 km of the surface in September of 1969. Then the trend reverses, and the minimum altitude begins trending higher. We see that there is a slower cycle of highs and lows superimposed on the 22 day cycle, which repeats about every 4 months. 

These cycles are very similar to the behavior of Snoopy's descent stage, and the cycles of eccentricity are can be explained by precession of the major axis of the orbit around the Moon. For whatever reason, the orbit always reaches it's highest eccentricity when the perilune point is above the near side of the moon. For Snoopy a cycle of precession takes about 25 days, while for the Eagle, in a lower orbit, it is about 22 days.

Now the big question. What happens if we run the simulation longer? When does the stage impact the moon? The answer, very surprisingly, is NEVER! I ran the simulation out to the present, which took about a week to complete on my home laptop. Here is a plot of the perilune points of the Eagle, simulated to the present...

Simulation of Eagle to the present shows no contact with the Moon!

The cycles of high and low eccentricity are almost completely lost in this graph, but there is no secular trend...the closest approach to the surface in 1969 is about the same as the closest approach in 2020. If the simulation is to be believed, then lunar gravity did not bring the Eagle down.

I have posted the simulation script and other information on GitHub, and I welcome you do try it yourself.

 It sounds crazy, but there is some possibility that the Eagle never impacted the Moon. Wouldn't it be amazing if we could find this amazing little vessel and bring her back to Earth!!!!