No one knows what became of the Eagle. That seems wrong.
After it carried Neil Armstrong and Buzz Aldrin back from the surface of the Moon in 1969, the ascent stage of the Apollo 11 Lunar Module "Eagle" was jettisoned into lunar orbit. The astronauts watched out the window as it drifted away. The NASA tracking network followed it for a few revolutions, until they lost the signal. Since then no one has seen or heard from the Eagle. Without question it is one of the most important machines ever created by humanity. Not knowing her fate is a terrible wrong which must be righted.
The assumption has always been that the Moon's lumpy gravity caused the Eagle's orbit to decay, and she impacted the Moon at an unknown location. In this post I will go through the last known orbital state of the Eagle, and show the results of simulating that orbit with the best gravity models available. Spoiler alert: as I found previously with "Snoopy", the orbit is quasi-stable. Lunar gravity alone may not have brought the Eagle down.
For the orbital state of the Eagle at the time it was jettisoned, we look to the Apollo 11 Mission Report. Table 7-II lists information about the spacecraft at various points in the mission, and in particular there is an entry for "Ascent stage jettison" as below.
 |
Orbital State of the Eagle at jettison, from the Mission Report
|
As I have described in a previous post, I use a simulation tool developed by NASA, and gravity models derived from GRAIL data. It's fairly straightforward to plug in the values from the table and simulate the stage. There is one problem with the Mission Report, though. It's wrong! When you think back to 1969, a world where word processing does not yet exist, and data processing is cumbersome, it isn't shocking that there is a problem in the table. But if you know a bit about the Apollo 11 orbit, the error is rather glaring.
All of the Apollo missions followed orbits that were low in inclination...that is, they stayed close to the lunar equator. It means that their "Space-fixed heading angle East of South" in degrees was never far from -90 degrees. If we use the value in the table, the orbit is inclined to the lunar equator by about 8 degrees...it can't be right.
What to do? Fortunately there is another source.
This paper from 1970 lists orbit data for several Apollo missions, including Apollo 11. In particular, it lists the inclination for several revolutions leading up to the moment the Eagle was cast off. By plotting out the values and extrapolating, one can find an accurate inclination at that moment...178.817 degrees. (Inclination would be 0 degrees for an orbit following the lunar equator, in the direction the Moon rotates. Because the orbit is "against" the rotation, the inclination is close to 180 degrees.) Using GMAT this inclination can be translated into a heading angle...-89.63 degrees.
 |
Extrapolating to find the inclination at the moment of jettison
|
Plugging this value into GMAT, along with the other values from table 7-II leads to a simulated orbit that matches up nicely to what is known about the mission. For instance the ground track of the orbit matches up well with those depicted in the Mission Report; the apolune and perilune values agree with values reported by Public Affairs Officer during the mission; and longitude values from the simulation agree well with Aquisition Of Signal and Loss Of Signal (AOS/LOS) times reported by tracking.
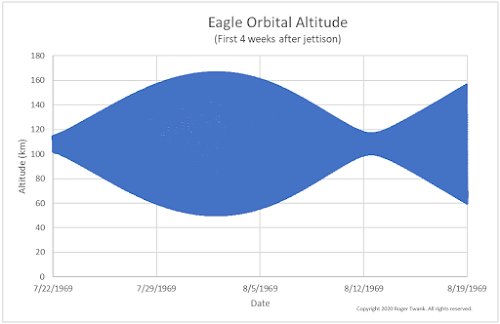
So what happens to our simulated Eagle? Let's look at the first five days after jettison. The stage was initially in an orbit that was "63.3 by 56 nautical miles", according to a P.A.O. announcement a few hours after jettison. That's a nearly circular orbit that is 117.2 kilometers at the high point and 103.7 km at the low point. From there we can see that our simulated stage is pulled into a more eccentric orbit, with higher highs and lower lows over the next 5 days.

If this trend were to continue, the Eagle would have indeed impacted the moon within a few weeks. However, as I have seen in previous simulations of Snoopy,
there is a pattern that takes hold, and the orbit cycles through periods of higher and lower eccentricity, completing one cycle about every 22 days. In the plot below we see that after about 10 days, the orbit begins to return to a more circular pattern, with lower highs and higher lows, until around August 13th, when it is nearly back to the original state. Then a new cycle begins and we see the minimum altitude dropping again.
For simplicity in the plots below, I will ignore the higher parts just focus on the lowest points of each orbit, following the lower envelope of the plot. If I plot out these low points (the "perilune" points) for the first year, we see that the orbit continues to oscillate throughout the year.
What is exciting about this simulation is that there is no impact! Across the first three cycles of eccentricity, the low point of the orbit drops down to within 20 km of the surface in September of 1969. Then the trend reverses, and the minimum altitude begins trending higher. We see that there is a slower cycle of highs and lows superimposed on the 22 day cycle, which repeats about every 4 months.
These cycles are very similar to the behavior of Snoopy's descent stage, and the cycles of eccentricity are can be explained
by precession of the major axis of the orbit around the Moon. For whatever reason, the orbit always reaches it's highest eccentricity when the perilune point is above the near side of the moon. For Snoopy a cycle of precession takes about 25 days, while for the Eagle, in a lower orbit, it is about 22 days.
Now the big question. What happens if we run the simulation longer? When does the stage impact the moon? The answer, very surprisingly, is NEVER! I ran the simulation out to the present, which took about a week to complete on my home laptop. Here is a plot of the perilune points of the Eagle, simulated to the present...
 |
Simulation of Eagle to the present shows no contact with the Moon!
|
The cycles of high and low eccentricity are almost completely lost in this graph, but there is no secular trend...the closest approach to the surface in 1969 is about the same as the closest approach in 2020. If the simulation is to be believed, then lunar gravity did not bring the Eagle down.
I have posted the simulation script and other information on
GitHub, and I welcome you do try it yourself.
It sounds crazy, but there is some possibility that the Eagle never impacted the Moon. Wouldn't it be amazing if we could find this amazing little vessel and bring her back to Earth!!!!